[Linear Algebra(선형대수)] 행렬(Matrix)이란?

1. 스칼라(scalar) / 벡터(vector)란? 

 행렬(matrix)을 알아보기에 앞서, 스칼라(scalra)와 벡터(vector)를 먼저 살펴보자.

행렬, determinant, eigenvalue, eigenvector, 
PCA 주경사분석
im2col alexnet resnet

 

1-1. 스칼라(scalar) / 벡터(vector)의 기하학적 의미

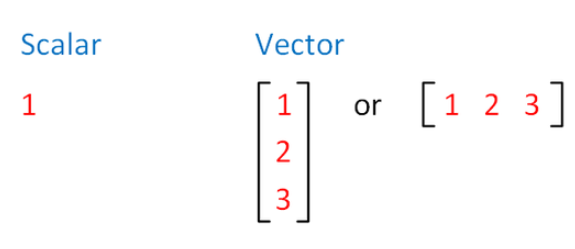
- 스칼라(scalar) : 크기만으로 완전히 표시될 수 있는 양 (only '크기')

   ex) 질량, 면적, 온도 등
   - 이탤릭체 소문자로 표시함.

- 벡터(vector) : 크기뿐만 아니라 방향성이 있어야 완전히 표시될 수 있는 양 ('크기' + '방향성', 'direction' + 'length') 

    ex) 힘 (force) : 어떤 물체에 같은 크기의 힘을 가해도, 가해진 방향에 따라 물체에 미친 효과가 다를 수 있음.
    - 볼드체 대문자로 표시함.

    - 2차원 및 3차원 공간에서 vector는 화살표(시작점 -> 끝점)로 표현 가능 (화살표의 길이는 벡터의 크기, 화살표의 방향은 벡터의 방향) 

    - 덧셈 및 스칼라배 가능

1 화살표로 표시되는 2-공간 및 3-공간에서의 벡터

  위의 기하학적 의미가 사실 쉽게 와닿지 않는데, scalar는 수, vector는 수의 나열(수를 일렬로 늘어놓은 1차원 배열;array)이라고 일단 간단히 생각하면 된다. (기하학적 의미는 형식상 적은 것이다.)

 

1-2. 벡터 = 공간 안의 점 

2-1 벡터를 공간 위에 표시

  위의 그림과 같이,  2차원 및 3차원 벡터를 공간 안에 점으로 표시할 수 있다. 이때, 영벡터는 모든 성분(component)가 0인 벡터로 원점(O)이라고 불리기도 한다. 

+) 위의 그림처럼 좌표의 원점 O를 시작점으로 공간 내의 임의의 한 점을 끝점으로 하는 벡터를  위치 벡터(position vector)라고 지칭한다.

2-2 벡터 덧셈 (이어붙임) & 스칼라배 (늘이고, 줄임)

  벡터를 화살표로 표현하면, 덧셈은 화살표의 이어붙임, 스칼라배는 길이를 늘이고, 줄임으로 생각할 수 있다. 

+) 벡터 덧셈의 삼각규칙 : 2- 공간 및 3-공간에서 두 벡터 a와 b가 b의 시작점과 a의 끝점이 같다면, 합인 a + b는 a의 시작점에서 b의 끝점을 잇는 화살표로 표현된 벡터임.)

 

1-3. 벡터 공간(vector space); 선형 공간(linear space)

3-1

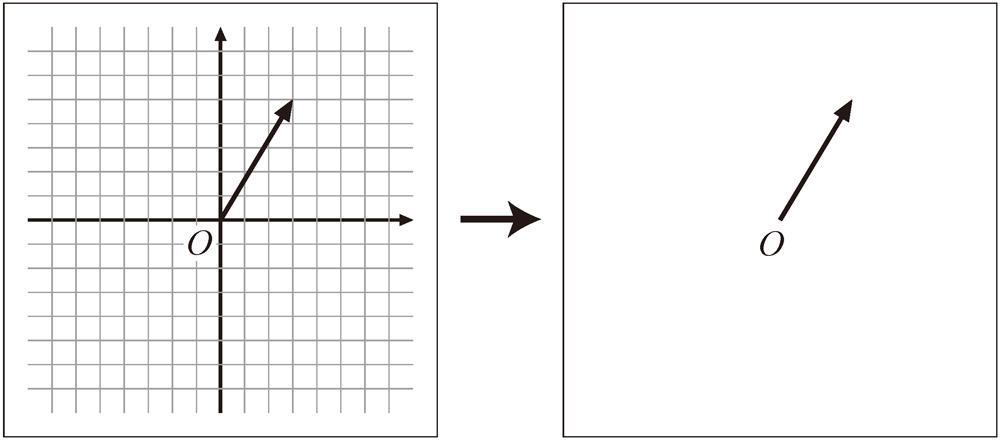
 위의 눈금그림에서 눈금을 지우고, 깨끗한 도화지(우주처럼 위인지 아래인지 특별한 '방향'이 없음)에 원점(O)만이 표식으로 두었을 때와 같이, '덧셈'과 '스칼라배'만 가능한 공간(space), 즉 덧셈과 스칼라배에 의해 닫혀 있는(closed under addition & multiplication) 공간을 벡터 공간(vector space), 혹은 선형 공간(linear space)이라 한다. 동일한 공간 내에 이는 벡터들 간 덧셈, 스칼라배한 결과 또한 해당 공간 내에 존재하기 때문에 닫혀있다고 표현한다.  해당 공간에서, 화살표는 (원점을 지나는) 직선형으로 표현되어야 한다.(즉, 선형성(linearity)를 만족해야한다.)

Q) 왜 원점(영벡터)을 지나는 직선이어야하는가?

A) 단순히 직선형이라고 선형성을 만족하는 것은 아니기 때문이다. f(x) = 3x + 2를 생각해보면, f(2x)와 2f(x)는 다르므로, 선형이 아니다.

선형성은 위의 두 조건을 동시에 만족해야 함.

 벡터 공간에서 가능한 연산인 덧셈과 스칼라배로 구성된 벡터들의 결합을 선형결합(linear combination)이라 한다.

선형결합

 선형결합를 통해 소수의 vector에 대하여 이어붙이고(덧셈), 늘이고, 줄여(스칼라배) 무한히 많은 vector를 만들 수 있다. 그래서 해당 공간(space) 내에서 무한히 많은 vector가 존재할 수 있다. (벡터 공간 내의 모든 vector들은 선형결합을 통해 만들어진다.) 

Q) 왜 원점(O)은 안 지우는가?

A) 영벡터, 즉 원점(O)은 공간(space)를 이루기 위해 반드시 포함되어야 하기 때문이다. 쉽게 생각해보았을 때, 벡터 v  x 0 = 0, 혹은 v + (-1)v = 0이므로,  0은 반드시 포함되어야 한다. 다르게 표현하자면, 영벡터가 없으면, 선형결합이 성립되지 않는 경우가 생길 수 있기(덧셈과 스칼라배를 정의할 수 없기) 때문이다.

벡터 공간은 아래와 같은 성질을 만족해야 한다.

1-4. 기저(basis, base)

   vector에 있어 중요한 것은 가리키는 점(끝점)이다. 만약 위치벡터(position vector)라면, 시작점이 원점임을 알기 때문에 끝점만 알면 해당 벡터의 방향과 길이는 자동으로 알 수 있다. (시작점에서 끝점을 그으면 알 수 있지 않은가)

그렇다면, 그림 3-1과 같이 원점만 표시되어 있는 (방향성이 없는) 깨끗한 하얀 도화지에서 끝점의 위치는 어떻게 지정할 수 있을까? 단순히 여기, 저기, 거기라고 할 수는 없으니 이때, 기저(basis, base) 개념을 도입한 것이다. 

  예를 들어, 주소 (ex) 서울특별시 서대문구 신촌동)를 통해 한국의 어디에 위치하고 있는지를 알 수 있는 것과 같은 기능을 기저가 한다는 것이다. 주소를 나타내기 위한 '시', '구', '동'이 basis라고 생각하면 좋다. 

선형대수학에서, 어떤 벡터 공간의 기저(basis)는 그 벡터 공간을 선형생성하는 선형독립인 벡터들이다. 달리 말해, 벡터 공간의 임의의 벡터에게 선형결합으로서 유일한 표현을 부여하는 벡터들이다. 
기저 (선형대수학) - 위키백과, 우리 모두의 백과사전 (wikipedia.org)

- 차원 안에 나타날 수 있는 모든 벡터들의 집합

+) span(생성) : 주어진 두 벡터의 조합으로 만들 수 있는 모든 가능한 벡터들의 집합, 주어진 벡터들의 선형조합을 통해 만들 수 있는 공간의 모음. basis와 반대로, 주어진 벡터를 통해 생성할 수 있는 공간, basis는 주어진 공간에서 만들어낼 수 있는 벡터들의 조합

- 선형결합이 unique함. 

- 기저 벡터의 개수 = 차원 (dimesnsion) = 좌표의 성분수

- 랭크(rank) : span의 차원 

 

선형독립과 선형종속에 관해서는 다른 포스트에서 알아보도록 하자...................

 

1-5. 텐서(Tensor) 

   텐서(tensor)는 선형대수에서 사용하는 데이터 배열;array을 지칭한 용어(a type of data structure used in linear algebra)이다. (유명한 deeplearning framework인 tensorflow의 그 tensor이다.)

  tensor의 랭크(rank)에 따라 구분될 수 있는데, rank=0일 때는 scalar, rank=1일 때는 vector, rank=2일 때는 행렬(matrix), 그리고 rank가 더 증가하면  n-차원 텐서(n-order tensor)로 부른다. 

TensorFlow for Deep Learning (dominicm73.blogspot.com)

2. 행렬(matrix)이란?

2-1. 행렬(matrix) = 사상(mapping)

   matrix은 mapping (vector가 공간 안의 점이라면, matrix은 공간에서 공간으로의 직교사상)이다. 이해를 돕기 위해, 함수(function) 개념을 통해 설명하자면,  변수 x에 f(x)를 적용한 경우, x값을 y값으로 변환해주는 f(x)의 역할과 matrix의 역할이 비슷하다고 생각하면 된다. 

   Ax = y (matrix는 대문자로 표시, A : matrix, x, y : vector)에서 행렬인 A는 벡터 x를 벡터 y로 옮기는 (n-차원 공간에서 m-차원 공간으로 옮기는) 사상이다.

- 행렬 = 사상, 즉 사상이 같다면, 행렬도 같다!
   같은 크기의 행렬 A, B가 임의의 벡터 x에 대해 항상 Ax = Bx 라면, A = B

 

2-2. 행렬의 곱 = 사상의 합성

 또, 함수와 함께 설명하자면, 합성함수 g(f(x))와 같이 B(Ax)처럼 생각하면 쉽다. 합성함수와 같이 A한 후, B하는 것이다. 

- BA  ≠ AB

 

2-2. 행렬의 거듭제곱 = 사상의 반복

 

참고

[Linear Algebra] Lecture 5 - (2) 벡터 공간(Vector Spaces), 부분 공간(Sub Spaces) :: Learn Again! 러너게인 (tistory.com)

[Linear Algebra] Lecture 5 - (2) 벡터 공간(Vector Spaces), 부분 공간(Sub Spaces)

[선형대수] 랭크(rank), 차원(dimension)의 의미 - 로스카츠의 AI 머신러닝 (losskatsu.github.io)

[선형대수] 랭크(rank), 차원(dimension)의 의미